Οι 5 μεγαλύτεροι δορυφόροι του ηλιακού μας συστήματος… στην ίδια αστροφωτογραφία

Στις φωτογραφίες που ακολουθούν, από αριστερά προς τα δεξιά, οι μικροσκοπικές φωτεινές κουκκίδες είναι ο Γανυμήδης, ο Δίας, η Ιώ, η Ευρώπη και η Καλλιστώ. Ο δικός μας φυσικός δορυφόρος φαίνεται πολύ μεγαλύτερος γιατί είναι κοντά, αλλά ο Γανυμήδης, η Ιώ και η Καλλιστώ στην πραγματικότητα μεγαλύτεροι από τη Σελήνη. Ο τέταρτος δορυφόρος του Δία που βλέπουμε, η Ευρώπη, είναι λίγο μικρότερος από την Σελήνη. Οι φωτογραφίες λήφθηκαν στις 3 Οκτωβρίου 2019, όταν ο Δίας και η Σελήνη βρέθηκαν πολύ κοντά στον νυχτερινό ουρανό. Από τους έξι μεγαλύτερους δορυφόρους των πλανητών του Ηλιακού Συστήματος, μόνο ο δορυφόρος του Τιτάνας του Κρόνου λείπει από αυτή τη φωτογραφία. Μπορείτε να δείτε τον Κρόνο απόψε στον νυχτερινό ουρανό, μιας και θα είναι πολύ κοντά (μια μοίρα) στη Σελήνη. Αν διαθέτετε τηλεσκόπιο ίσως μπορέσετε να διακρίνετε τον δεύτερο κατά σειρά μεγέθους δορυφόρο στο πλανητικό μας σύστημα, τον Τιτάνα του Κρόνου.

Credit : Derek Demeter Lake Mary, Florida

Gredit: Roberto Colombari

Credit : jordiler

Credit: Νικ Pavelchak

Credit: Valerio Fontani

Ποιος είναι ο νόμος του Faraday;

 Η «κινησιακή» ηλεκτρεγερτική δύναμη και ο κανόνας ροής)

Το 1831 ο Michael Faraday παρουσίασε μια σειρά από πειράματα, τρία εκ των οποίων μπορούν να περιγραφούν ως εξής (με μια μικρή αλλοίωση της ιστορίας):

Πείραμα 1: Παρουσία ενός μαγνητικού πεδίου, μετακινούμε έναν αγώγιμο βρόχο προς τα δεξιά – βλέπε σχήμα (a). Στον βρόχο δημιουργήθηκε ροή ρεύματος.
Πείραμα 2: Κρατώντας τον βρόχο ακίνητο, μετακινούμε τον μαγνήτη (άρα και το μαγνητικό του πεδίο) προς τα αριστερά – βλέπε σχήμα (b). Δημιουργήθηκε πάλι ροή ρεύματος στο  στον βρόχο.
Πείραμα 3: Κρατώντας ακίνητο και τον βρόχο και τον μαγνήτη – σχήμα (c) – μεταβάλλουμε την ένταση του μαγνητικού πεδίου (χρησιμοποιώντας έναν ηλεκτρομαγνήτη μεταβάλλοντας την ένταση του ρεύματος του πηνίου). Για άλλη μια φορά δημιουργήθηκε ρεύμα στον βρόχο.

Το πρώτο πείραμα είναι ένα παράδειγμα κινησιακής ΗΕΔ, που εκφράζεται από τον κανόνα της ροής: Ɛ=–dΦ/dt.
Δε νομίζω να εκπλαγείτε αν σας πω ότι η ίδια ακριβώς ΗΕΔ αναπτύσσεται και στο πείραμα 2 – το μόνο που έχει σημασία είναι η σχετική κίνηση του μαγνήτη και του βρόχου.

Πράγματι, από την σκοπιά της Ειδικής Σχετικότητας πρέπει να είναι έτσι. Αλλά ο Faraday δεν γνώριζε σχετικότητα, και στην κλασσική ηλεκτροδυναμική αυτή η απλή αμοιβαιότητα είναι μια αξιοσημείωτη σύμπτωση. Στην περίπτωση του κινούμενου βρόχου, είναι μια μαγνητική δύναμη που κινεί τα φορτία και προκαλεί την ΗΕΔ, αλλά όταν ο βρόχος είναι ακίνητος η δύναμη που είναι υπεύθυνη για την εμφάνιση της ΗΕΔ δεν μπορεί να είναι μαγνητική – σε ακίνητα φορτία δεν ασκούνται μαγνητικές δυνάμεις. Τι είναι λοιπόν αυτό που προκαλεί την ΗΕΔ στην περίπτωση αυτή; Ποιο είναι το είδος του πεδίου που ασκεί δύναμη στα ακίνητα φορτία; Προφανώς κάποιο ηλεκτρικό πεδίο, αλλά σ’ αυτή την περίπτωση δεν φαίνεται κάποιο ηλεκτρικό πεδίο. Ο Faraday είχε μια ευφυή έμπνευση:

Ένα μεταβαλλόμενο μαγνητικό πεδίο  δημιουργεί επαγωγικά ένα ηλεκτρικό πεδίο.

Σε αυτό το επαγόμενο ηλεκτρικό πεδίο οφείλεται η ΗΕΔ του δεύτερου πειράματος (Εδώ μπορεί κάποιος να υποστηρίξει ότι το μαγνητικό πεδίο στο πείραμα 2 δεν αλλάζει πραγματικά – απλά κινείται. Αυτό που εννοώ είναι ότι αν σταθείτε σε μια σταθερή θέση το πεδίο που θα ανιχνεύσετε μεταβάλλεται καθώς διέρχεται ο μαγνήτης).

Πράγματι, αν (όπως ανακάλυψε πειραματικά ο Farady) η ΗΕΔ ισούται πάλι με τον ρυθμό μεταβολής της ροής:

 ή 

Γράψαμε το νόμο του Faraday σε ολοκληρωτική μορφή όπου φαίνεται πως το 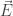 σχετίζεται με το  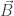(Παρατηρείστε ότι αν το μαγνητικό πεδίο είναι σταθερό παίρνουμε  όπως ισχύει στην στατική περίπτωση).

Στο πείραμα 3 το μαγνητικό πεδίο μεταβάλλεται για εντελώς διαφορετικούς λόγους, αλλά σύμφωνα με το νόμο του Faraday επάγεται πάλι ένα ηλεκτρικό πεδίο το οποίο θα δημιουργήσει μια ΗΕΔ –dΦ/dt. Έτσι, μπορούμε να συμπτύξουμε και τις τρεις περιπτώσεις (και οποιονδήποτε συνδυασμό τους) σε ένα είδος παγκόσμιου κανόνα της ροής:

Οποτεδήποτε (και για οποιονδήποτε λόγο) μεταβάλλεται η μαγνητική ροή που διέρχεται μέσα από έναν βρόχο, μια ΗΕΔ

 Ɛ=–dΦ/dt               (1)

εμφανίζεται στον βρόχο.

Πολλοί ονομάζουν την διατύπωση αυτή «νόμο του Faraday». Μπορεί να γίνομαι σχολαστικός, αλλά αυτό μου προκαλεί σύγχυση. Στην πραγματικότητα υπάρχουν δυο εντελώς διαφορετικοί μηχανισμοί πίσω από την εξ. (1) και με το να τους ταυτίζουμε και τους δυο με τον «νόμο του Faraday» είναι σα να λέμε ότι εφόσον τα δυο δίδυμα μοιάζουν θα πρέπει να τα φωνάζουμε με το ίδιο όνομα.

Στο πρώτο πείραμα του Faraday είναι η δύναμη Lorentz που δρα και η ΗΕΔ είναι μαγνητική. Αλλά στα επόμενα δυο πειράματα είναι ένα ηλεκτρικό πεδίο (επαγόμενο από την μεταβολή του μαγνητικού πεδίου) που κάνει τη δουλειά. Κάτω από αυτό το πρίσμα, είναι μάλλον απροσδόκητο το ότι και η πρώτη διαδικασία παράγει την ίδια σχέση για την ΗΕΔ με τις επόμενες δύο. Στην πραγματικότητα, ήταν ακριβώς αυτή η «σύμπτωση» που οδήγησε τον Einstein στην ειδική θεωρία της σχετικότητας – προσπάθησε να βρεί μια βαθύτερη ερμηνεία του γεγονότος που αποτελούσε σύμπτωση στην κλασσική ηλεκτροδυναμική. Αλλά αυτό είναι μια ιστορία της ειδικής σχετικότητας. Όταν λοιπόν βρισκόμαστε στα χωράφια της κλασσικής ηλεκτροδυναμικής,  και μέχρι να φτάσουμε στην θεωρία της ειδικής σχετικότητας, καλό είναι να κρατήσουμε τον όρο «νόμος του Faraday» για τα ηλεκτρικά πεδία που επάγονται από μεταβαλλόμενα μαγνητικά πεδία, μη θεωρώντας το πείραμα 1 ως περίπτωση του νόμου Faraday.

πηγή: «Εισαγωγή στην Ηλεκτροδυναμική», David J. Griffiths, Πανεπιστημιακές Εκδόσεις Κρήτης

Ψάχνοντας για σκουληκότρυπες

Μια πρόσφατη μελέτη μας δείχνει πως θα μπορούσαμε να ανιχνεύσουμε τα αστρονομικά αντικείμενα που εξιτάρουν την φαντασία των φίλων της επιστημονικής φαντασίας. Τις σκουληκότρυπες.

Η σκουληκότρυπα στην εικόνα σχηματίζει μια συντομότερη διαδρομή μεταξύ δυο απομακρυσμένων περιοχών του σύμπαντος.

Το 1916, έναν χρόνο μετά την διατύπωση της γενικής θεωρίας της σχετικότητας , o Ludwig Flamm ανακάλυψε μια λύση των εξισώσεων του Eisntein που περιέγραφε αυτό που σήμερα ονομάζουμε σκουληκότρυπα. Πρόκειται για μια τοπολογική ιδιότητα του χωροχρόνου βάσει της οποίας σχηματίζεται ένα «τούνελ» που συνδέει δύο απομακρυσμένα σημεία του – ένα «κόψιμο δρόμου» διαμέσου του χωρόχρονου. Τον όρο «σκουληκότρυπα» εμπνεύστηκε ο John Archibald Wheeler, από τις σκουληκότρυπες των μήλων.

Για μια απλή οπτική εξήγηση της σκουληκότρυπας, φανταζόμαστε τον χωρόχρονο να απεικονίζεται ως μία δισδιάστατη επιφάνεια. Αν αυτή η επιφάνεια καμπυλωθεί διαμέσου μιας τρίτης διάστασης, μας δίνει την εικόνα της σκουληκότρυπας σαν έναν «σωλήνα» που ενώνει δύο απομακρυσμένες περιοχές του χωρόχρονου. Στην πραγματικότητα αυτή η δισδιάσταστη επιφάνεια είναι τετραδιάστατη (τρεις διαστάσεις χώρου + μία χρόνου) και γι αυτό η οπτικοποίηση της πραγματικής καμπυλότητας είναι αδύνατη. Προς το παρόν δεν υπάρχουν παρατηρησιακά δεδομένα για σκουληκότρυπες, οι οποίες όμως προβλέπονται από την Γενική θεωρία της Σχετικότητας.

α) Διάγραμμα μιας σκουληκότρυπας που συνδέει δυο διαφορετικά σύμπαντα
(β) Διάγραμμα σκουληκότρυπας που συνδέει δυο απομακρυσμένες περιοχές του σύμπαντος.

Το αν υπάρχουν οι σκουληκότρυπες μπορεί να είναι υπό συζήτηση, όμως κανείς δεν απαγορεύει τους φυσικούς να ψάχνουν τρόπους για να τις ανιχνεύσουν, στην περίπτωση που υπάρχουν.
Κι αυτό κάνουν οι De-Chang Dai και Dejan Stojkovic στο άρθρο τους με τίτλο «Observing a wormhole».
Η μέθοδός τους επικεντρώνεται στον εντοπισμό μιας σκουληκότρυπας γύρω από τον Τοξότη Α*, ένα αντικείμενο που θεωρείται πως είναι μια υπερμεγέθης μαύρη τρύπα στο κέντρο του Γαλαξία μας. Ενώ δεν υπάρχουν αποδείξεις ότι εκεί υπάρχει μια σκουληκότρυπα, πρόκειται για την κατάλληλη θέση αναζήτησης, διότι η ύπαρξη σκουληκότρυπας απαιτεί ισχυρά βαρυτικά πεδία, σαν αυτά που υπάρχουν στις υπερμεγέθεις μαύρες τρύπες.

Οι Dai και Stojkovic υποστηρίζουν ότι αν υπάρχει μια σκουληκότρυπα στον Τοξότη Α*, τα κοντινά σ’ αυτήν άστρα θα επηρεάζονται από την βαρύτητα των άστρων που υπάρχουν στο άλλο άκρο της σκουληκότρυπας. Επομένως, αναζητώντας μικρές αποκλίσεις στην αναμενόμενη τροχιά των άστρων στην γειτονιά του Τοξότη Α*, θα ήταν δυνατόν να ανιχνευθεί η ύπαρξη της σκουληκότρυπας

Σύμφωνα με τον Dejan Stojkovic: «αν έχετε δύο άστρα, ένα σε κάθε πλευρά της σκουληκότρυπας, το άστρο που βρίσκεται στην πλευρά μας θα πρέπει να αισθάνεται την βαρυτική αλληλεπίδραση από το άστρο που βρίσκεται στην απέναντι πλευρά. Η βαρυτική ροή θα περνάει μέσα από τη σκουληκότρυπα. Επομένως, θα εμφανίζονται αποκλίσεις στην αναμενόμενη τροχιά ενός άστρου γύρω από τον Τοξότη Α*, εφόσον εκεί υπάρχει σκουληκότρυπα με ένα άλλο άστρο στην άλλη πλευρά της».

Εστιάζοντας στο S2, ένα άστρο που περιφέρεται γύρω από τον Τοξότη A*

Ο Stojkovic υποστηρίζει πως αν ποτέ βρεθούν σκουληκότρυπες, δεν θα είναι σαν αυτές που περιγράφονται από την επιστημονική φαντασία. Ισχυρίζεται πως οι άνθρωποι και τα διαστημόπλοια πιθανότητα δεν θα μπορούν να τις διασχίσουν. Απαιτείται μια πηγή αρνητικής ενέργειας για να διατηρηθεί η σκουληκότρυπα ανοιχτή, και δεν ξέρουμε πως μπορούμε να πετύχουμε κάτι τέτοιο. Η δημιουργία μιας σκουληκότρυπας που θα παραμένει σταθερή φαίνεται (προς το παρόν) εξωπραγματική.

Παρ’ όλα αυτά, οι σκουληκότρυπες – είτε μπορούμε να τις διασχίσουμε είτε όχι – είναι ένα από τα πιο ενδιαφέροντα θεωρητικά φυσικά φαινόμενα για μελέτη. Μπορεί να μην έχουν ανιχνευθεί, σύμφωνα όμως με την θεωρία είναι δυνατή η ύπαρξή τους. Οι σκουληκότρυπες, λέει ο Stojkovic, «είναι μια νόμιμη λύση των εξισώσεων του Αϊνστάιν».

Στην εργασία τους οι Stojkovic και Dai επικεντρώνονται στο πως θα μπορούσαμε να εντοπίσουμε μια σκουληκότρυπα αναζητώντας διαταραχές στην τροχιά του άστρου S2, που περιφέρεται γύρω από τον Τοξότη A*.

Ενώ οι σημερινές τεχνικές παρακολούθησης δεν είναι ακόμα αρκετά ακριβείς για να αποκαλύψουν την παρουσία μια σκουληκότρυπας, οι Stojkovic και Dai υποστηρίζουν ότι η συλλογή δεδομένων για το S2 για ένα μεγαλύτερο χρονικό διάστημα ή η ανάπτυξη τεχνικών για την ακριβέστερη παρακολούθηση της κίνησης, θα καθιστούσε δυνατή μια τέτοια ανίχνευση. Κι αυτό θα μπορούσε να συμβεί στα επόμενα δέκα με είκοσι χρόνια από σήμερα.

Ωστόσο, ακόμα κι αν με τον έναν ή τον άλλο τρόπο ανιχνεύσουμε διαταραχές στην τροχιά του S2, δεν θα μπορούμε να τις αποδώσουμε με βεβαιότητα σε μια σκουληκότρυπα. Θα μπορούσε πιθανόν να υπάρχει κάποια άλλη αιτία στην δική μας πλευρά που διαταράσσει την κίνηση αυτού του άστρου.
Αν και η εργασία επικεντρώνεται στις διαπερατές σκουληκότρυπες, η μέθοδος θα μπορούσε να δείχνει την παρουσία και μη διαπερατής σκουληκότρυπας. Διότι σύμφωνα με τον Stojkovic η επίδραση της βαρύτητας γίνεται αισθητή και στις δυο πλευρές της σκουληκότρυπας, είτε αυτές διασχίζονται από αντικείμενα είτε όχι.

πηγή: http://www.buffalo.edu/news/releases/2019/10/035.html

Το διαστημικό τηλεσκόπιο Hubble φωτογραφίζει διαστρικό κομήτη

Το διαστημικό τηλεσκόπιο Hubble της NASA κατάφερε να καταγράψει την καλύτερη έως τώρα εικόνα του διαστρικού κομήτη 2I/Borisov ή C/2019 Q4 (Borisov). Η ταχύτητα και η τροχιά του κομήτη επιβεβαιώνουν ότι προέρχεται έξω από το δικό μας ηλιακό σύστημα.
Η φωτογραφία του Hubble λήφθηκε στις 12 Οκτωβρίου 2019. Ο κομήτης απείχε απόσταση 260 εκατομμυρίων μιλίων από τη Γη και κατευθύνεται προς τον Ήλιο. Η ταχύτητά του τώρα είναι 110.000 μιλίων την ώρα. Στις 7 Δεκεμβρίου 2019 θα περάσει από την πλησιέστερη στον ήλιο απόσταση, περίπου δυο φορές την απόσταση Γης – ήλιου.
Ο κομήτης 2I/Borisov είναι το δεύτερο διαστρικό αντικείμενο που γνωρίζουμε ότι έχει περάσει μέσα από το ηλιακό μας σύστημα. Το 2017, διαπιστώθηκε ο πρώτος διαστρικός επισκέπτης, ένα αντικείμενο που ονομάστηκε Οουμουαμούα.

πηγή: https://www.nasa.gov/feature/goddard/2019/hubble-observes-1st-confirmed-interstellar-comet