ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ
1) Σώμα εκτοξεύεται από ύψος h = 180m πάνω από το έδαφος, με οριζόντια ταχύτητα μέτρου u0 = 40m/s.
Να βρείτε:
i) την ταχύτητα του σώματος (κατά μέτρο και
κατεύθυνση), όταν το σώμα, βρίσκεται σε ύψος h’ =45m πάνω από το έδαφος, και την οριζόντια απόσταση στη θέση αυτή.
ii) το χρόνο καθόδου.
iii) την ταχύτητα (κατά μέτρο και κατεύθυνση) του
σώματος όταν χτυπά στο έδαφος.
iv) την οριζόντια απόσταση (βεληνεκές), όταν χτυπά στο έδαφος.
2) Από ένα σημείο
Ο που βρίσκεται σε ύψος h=80m από το έδαφος, εκτοξεύεται οριζόντια ένα σώμα Α,
με αρχική ταχύτητα υ0 =30m/s, ενώ ταυτόχρονα αφήνεται να πέσει (από
το Ο) ένα δεύτερο σώμα Β.
i) Πού βρίσκονται τα
δύο σώματα μετά από 2s;
ii) Σε πόσο χρόνο
κάθε σώμα θα φτάσει στο έδαφος;
iii) Σε ποιο σημείο
το σώμα Α θα πέσει στο έδαφος και ποια η ταχύτητά του, την στιγμή εκείνη;
iv) Να βρεθεί η
μετατόπιση του σώματος Α, μέχρι να φτάσει στο έδαφος.
Δίνεται g=10m/s2 , ενώ η αντίσταση του αέρα
θεωρείται αμελητέα.
3) Δύο κτήρια
απέχουν 30m. Από το ψηλότερο Α, που έχει ύψος Η=60m, εκτοξεύεται οριζόντια μια
μπάλα με αρχική ταχύτητα υ0 =10m/s, με σκοπό να φτάσει στην ταράτσα
του χαμηλότερου κτηρίου Β, που έχει ύψος h=40m και πλάτος α=10m.
i) Θα φτάσει η μπάλα
στην ταράτσα του Β κτηρίου;
ii) Για ποιες τιμές της ταχύτητας η μπάλα θα πέσει στην
ταράτσα του Β κτηρίου;
iii) Εκτοξεύουμε οριζόντια την μπάλα με ταχύτητα υ01
=22m/s. Θα μπορέσει να την πιάσει ένα παιδί, που βρίσκεται στην ταράτσα του Β
κτηρίου, αν έχει την ικανότητα πηδώντας, να την σταματήσει ακόμη και σε ύψος
2,8m; Η αντίσταση του αέρα θεωρείται αμελητέα ενώ g=10m/s2 .
4) Ένα σώµα
εκτοξεύεται οριζόντια µε αρχική ταχύτητα υ0, από ορισµένο ύψος και µετά από
λίγο βρίσκεται σε σηµείο Α, έχοντας μετακινηθεί κατά 20m οριζόντια και κατά 5m
κατακόρυφα.
i) Ποια η αρχική
ταχύτητα εκτόξευσης υ0 ;
ii) Βρείτε την
ταχύτητα του σώµατος στο σηµείο Α.
iii) Ποια γωνία έχουμε µεταξύ επιτάχυνσης και ταχύτητας στο
Α;
iv) Τη στιγµή που το σώµα φτάνει στο έδαφος η ταχύτητά του
σχηµατίζει γωνία 45° µε τον ορίζοντα. Από ποιο ύψος έγινε η εκτόξευση του
σώµατος;
∆ίνεται g=10m/s2 .
5) Από ένα σημείο
Ο στην ταράτσα ενός ψηλού κτηρίου σε ύψος Η=80m, εκτοξεύεται οριζόντια ένα σώμα
μάζας m=0,2kg με αρχική ταχύτητα υ0 =20m/s τη στιγμή t0 =0.
Η αντίσταση του αέρα θεωρείται αμελητέα ενώ g=10m/s2 .
i) Ποια χρονική
στιγμή το σώμα περνάει από ένα σημείο Α που βρίσκεται σε ύψος h=60m από το
έδαφος;
ii) Να βρεθεί η ταχύτητα του σώματος στη θέση Α.
iii) Να υπολογιστεί η
μεταβολή της ταχύτητας του σώματος μεταξύ των σημείων Ο και Α.
iv) Ποιος ο ρυθμός μεταβολής της ταχύτητας στη θέση Α;
v) Να βρεθεί η ισχύς του βάρους στην παραπάνω θέση.
6) Από ορισμένο
ύψος Η από το έδαφος, εκτοξεύεται ένα σώμα μάζας 0,1kg οριζόντια με ταχύτητα υ0
. Μετά από χρονικό διάστημα 2s, το σώμα βρίσκεται σε σημείο Α έχοντας ταχύτητα
25m/s απέχοντας κατά 6m από το έδαφος.
Αν g=10m/s2
ενώ η αντίσταση του αέρα θεωρείται αμελητέα να υπολογιστούν:
i) Η αρχική ταχύτητα
και το αρχικό ύψος από το οποίο έγινε η εκτόξευση.
ii) Το έργο του βάρους στο χρονικό διάστημα των 2s.
iii) Η μέση ισχύς του βάρους από 0-2s και η (στιγμιαία)
ισχύς του στη θέση Α.
iv) Ο ρυθμός
μεταβολής της δυναμικής ενέργειας και ο αντίστοιχος ρυθμός μεταβολής της
κινητικής ενέργειας στη θέση Α.
ΑΣΚΗΣΕΙΣ
1)
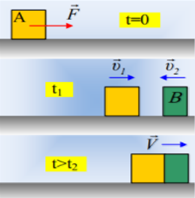
Μια ομάδα μαθητών, θέλοντας να μελετήσει την αρχή διατήρησης ορμής κατά τη διάσπαση ενός συστήματος σωμάτων, έφτιαξε τη διάταξη του σχήματος, που μοιάζει με πύραυλο και αποτελείται από τρία σώματα, σε επαφή μεταξύ τους, που ηρεμούν πάνω σε λείο οριζόντιο δάπεδο. Το μεσαίο σώμα Σ2 έχει μάζα Μ = 6Kg και τα ακραία Σ1 και Σ3 έχουν ίσες μάζες m = 2kg το καθένα. Μεταξύ των σωμάτων τοποθέτησαν ελάχιστη ποσότητα εκρηκτικού υλικού και φυτίλια κατάλληλου μήκους, τα οποία και άναψαν, ώστε να πυροδοτήσουν διαδοχικά τα εκρηκτικά σε καθορισμένες χρονικές στιγμές.
Τη χρονική στιγμή t0 = 0, το Σ1 εκτοξεύεται προς τα αριστερά, με ταχύτητα μέτρου |υ1| = 4m/s, ενώ τη χρονική στιγμή t1 =0,8s, το Σ3 εκτοξεύεται προς τα δεξιά, με ταχύτητα μέτρου |υ3| =5m/s. Οι ταχύτητες είναι μετρημένες από έναν ακίνητο παρατηρητή, οι εκρήξεις διαρκούν αμελητέο χρονικό διάστημα και η αντίσταση του αέρα θεωρείται αμελητέα.
α) Ποια είναι η ταχύτητα του τμήματος Σ2-Σ3, αμέσως μετά την εκτόξευση του Σ1;
β) Ποια είναι η ταχύτητα του Σ2 αμέσως μετά την εκτόξευση του Σ3;
γ) Ποιο είναι το συνολικό ποσό της ενέργειας που εκλύθηκε από τα εκρηκτικά, αν το 45,3% αυτής έγινε θερμότητα και ακτινοβολία;
δ) Ποια θα είναι η μετατόπιση κάθε σώματος τη χρονική στιγμή t2 = 2,8s;
ε) Ποια θα έπρεπε να είναι η ταχύτητα εκτόξευσης του Σ3 ώστε το Σ2 να ακινητοποιηθεί;
2)
Δύο σφαιρικά σώματα Σ1 και Σ2 με μάζες m1 και m2 αντίστοιχα κινούνται πάνω σε οριζόντιο δάπεδο και συγκρούονται κεντρικά και πλαστικά.Ελάχιστα πριν την σύγκρουση τα δύο σώματα κινούνται με αντίθετη φορά,έχοντας ταχύτητες μέτρων υ1=20m/s και υ2 .Η μεταβολή της ορμής της σφαίρας Σ2 κατά την κρούση έχει αλγεβρική τιμή




ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
1. Ένα ποδήλατο διαγράφει κύκλο ακτίνας R
=5m, με σταθερή ταχύτητα σε χρόνο Τ =2s.
Να βρεθούν:
i.
η γωνιακή
ταχύτητα ω και
ii. η γραμμική ταχύτητα υ.
Δίνεται
π = 3,14
Απ. ω =
3,14 rad/s , υ = 15,7m/s
2. Τροχός ακτίνας R1 =0,2m περιστρέφεται με συχνότητα
f1=5Hz
και καθώς συνδέεται με ιμάντα με τον τροχό ακτίνας R2 =0,4m, τον θέτει σε περιστροφή. Να
υπολογίσετε
i.
τις
γωνιακές ταχύτητες των τροχών
ii.
την
ταχύτητα του ιμάντα
Απ.
31,4 & 15,7 rad/s
, 6,28 m/s
3. Από δύο αντιδιαμετρικά
σημεία Α και Β ενός στίβου ξεκινούν συγχρόνως δύο δρομείς με ταχύτητες υ1
και υ2 και με αντίθετες διευθύνσεις . Οι δύο δρομείς συναντώνται για
πρώτη φορά στο σημείο Κ του στίβου, τέτοιο ώστε το τόξο ΒΚ να έχει μήκος 120m και για δεύτερη φορά στο σημείο Λ του
στίβου, ώστε το τόξο ΑΛ να έχει μήκος 60m. Αν ανάμεσα στις συναντήσεις μεσολαβεί
χρόνος 60sec,
να βρεθούν ;
i. Το
μήκος του στίβου και
ii. Οι
ταχύτητες υ1 και υ2
Απ. 600m ,
6m/sec , 4m/sec ή 360m ,
2m/s , 4m/sec
4. Δύο περιφέρειες εφάπτονται εξωτερικά και έχουν ακτίνες R1=5m και R2=6m.
Από το σημείο επαφής Α αναχωρούν δύο κινητά με ταχύτητες υ1 = 3m/s και υ2 =6m/s, που κινούνται πάνω στις περιφέρειες.
i.
Όταν θα
συναντηθούν για πρώτη φορά στο Α πόσες στροφές θα έχει κάνει κάθε κινητό;
ii.
Πόσο χρόνο
μετά θα γίνει η συνάντηση στο Α.
Απ.
N1 = 3 , N2 = 5 , 10π s
5. Δύο μικρές σφαίρες ίσων μαζών συνδέονται με
νήμα που είναι περασμένο από μικρή οπή λείου οριζόντιου τραπεζιού. Η μία σφαίρα
είναι πάνω στο τραπέζι και η άλλη κρέμεται κατακόρυφα από το νήμα κάτω από το
τραπέζι. Με ποια συχνότητα πρέπει να περιστρέφεται η σφαίρα πάνω στο τραπέζι σε
κυκλική τροχιά ακτίνας 0,16m
ώστε η άλλη να ηρεμεί;
Δίνεται g =10m/s2.
Απ. 1,25Ηz
6. Λείο
ημισφαίριο, ακτίνας R = 5m είναι
στερεωμένο στο δάπεδο έτσι ώστε να στρέφει τα κοίλα προς τα πάνω, με τον άξονα
του είναι κατακόρυφο.
Αφήνουμε μικρή σφαίρα μάζας m
= 2kg να
γλιστρήσει από το χείλος του ημισφαιρίου.
i.
Ποια θα
είναι η ταχύτητα της σφαίρας όταν φτάνει στο κατώτερο σημείο της τροχιάς της.
ii.
Πόση δύναμη
δέχεται η σφαίρα από το ημισφαίριο;
Δίνεται g =10m/s2
Απ. 10m/s , 60N
7. Αυτοκίνητο στρίβει σε
οριζόντιο κυκλικό δρόμο ακτίνας R = 100m. Αν ο συντελεστής τριβής μεταξύ ελαστικών και οδοστρώματος είναι
μ = 0,4 , να υπολογίσετε την μέγιστη
ταχύτητα με την οποία μπορεί το αυτοκίνητο να πάρει τη στροφή χωρίς να
γλιστρήσει. Δίνεται g= 10m/s2
Απ.
20m/s
8. Από την κορυφή λείου κεκλιμένου επιπέδου αφήνουμε
σώμα το οποίο όταν φτάνει στην βάση του εισέρχεται στο λείο ημικύκλιο του σχήματος. Στο
ανώτερο σημείο Α η δύναμη που δέχεται το σώμα από το ημικύκλιο έχει μέτρο FA= 3mg, όπου m η μάζα του σώματος. Από το σημείο Α και μετά το
σώμα εκτελεί οριζόντια βολή και την στιγμή που συγκρούεται με το κεκλιμένο
επίπεδο η ταχύτητά του είναι κάθετη σε αυτό.
Το
ημικύκλιο έχει ακτίνα R η οποία να θεωρηθεί γνωστή και η γωνία του
κεκλιμένου επιπέδου είναι φ = 600, επίσης η επιτάχυνση της βαρύτητας
είναι g.
i. Να βρεθεί το ύψος Η από το οποίο
αφήσαμε το σώμα.
ii. Να βρεθεί το χρονικό διάστημα της
οριζόντιας βολής.
iii. Σε πόσο ύψος h1 από το έδαφος βρίσκεται το σημείο
σύγκρουσης του σώματος με το κεκλιμένο επίπεδο;
iv. Την στιγμή που ξεκινά η
οριζόντια βολή από την κορυφή του κεκλιμένου επιπέδου και από ύψος Η
εκτοξεύουμε δεύτερο σώμα με αρχική ταχύτητα υ0 παράλληλη στο κεκλιμένο επίπεδο ,έτσι ώστε να συναντήσει το πρώτο
σώμα την στιγμή που συγκρούεται με το κεκλιμένο επίπεδο. Να βρεθεί η
ταχύτητα υ0.
9.Ένα
σώμα μάζας 2kg ηρεμεί δεμένο στο άκρο κατακόρυφου νήματος μήκους ℓ=1m, το άλλο
άκρο του οποίου είναι δεμένο σε σταθερό σημείο Ο. Σε μια στιγμή, ασκούμε στο
σώμα μια δύναμη F, εφαπτομενικά, μέχρι να φτάσει τη θέση Β,
όπου το νήμα γίνεται οριζόντιο. Στη θέση Β η δύναμη F παύει να ασκείται, ενώ το
έργο της για την παραπάνω μετακίνηση είναι ίσο με 100J.
i i. Να υπολογίσετε το έργο του βάρους για την κίνηση από τη θέση
Α στη θέση Β.
i ii. Πόση είναι η κινητική ενέργεια του σώματος στη θέση Β;
i iii. Να υπολογίσετε την τάση του νήματος στις θέσεις Α και Β.
i iv. Ποια η ελάχιστη κινητική ενέργεια που θα αποκτήσει στη
συνέχεια κατά την περιστροφή του το σώμα και πόση θα είναι τη στιγμή αυτή η
τάση του νήματος;
v. Να υπολογιστεί το μέτρο της δύναμης F, αν παραμένει σταθερό.
Δίνεται
g=10m/s2
ΟΡΜΗ
ΟΡΜΗ
Ερωτήσεις τύπου (Σ-Λ) + Πολλαπλής
επιλογής + Συμπλήρωσης
1. Α) Ένα σύστημα
σωμάτων είναι δυνατό να έχει κινητική ενέργεια χωρίς να έχει ορμή.
Β) Ένα σύστημα σωμάτων είναι δυνατό να έχει ορμή
χωρίς να έχει κινητική ενέργεια.
2. Ποιο από τα παρακάτω μεγέθη διατηρείται σε κάθε
κρούση;
Α) Η κινητική ενέργεια του
συστήματος.
Β) Η μηχανική του ενέργεια.
Γ) Η ορμή του.
3. Α) Μετά την
ελαστική κρούση δύο σφαιρών είναι δυνατόν και οι δύο σφαίρες να είναι ακίνητες.
Β) Μετά την πλαστική κρούση δύο
σφαιρών είναι δυνατόν το συσσωμάτωμα να παραμένει ακίνητο.
4.
Δύο σώματα συγκρούονται κεντρικά και πλαστικά. Αν το συσσωμάτωμα μετά την
κρούση παραμένει ακίνητο, αυτό σημαίνει ότι :
Α) Τα σώματα, πριν την κρούση, έχουν ίσες κινητικές ενέργειες
Β) Η συνολική ορμή του συστήματος, πριν την κρούση, είναι μηδέν.
Γ) Τα σώματα, πριν την κρούση, έχουν αντίθετες ταχύτητες.
Δ) Ένα μέρος της αρχικής κινητικής ενέργειας των σωμάτων μετατράπηκε σε
θερμότητα.
5. Α) Όταν δύο σώματα συγκρούονται ελαστικά δεν
απελευθερώνεται θερμότητα.
Β) Όταν δύο σώματα της ίδιας μάζας,
που κινούνται σε αντίθετες κατευθύνσεις με ίσου μέτρου ταχύτητες, συγκρουστούν
μετωπικά και ελαστικά, ακινητοποιούνται μετά την κρούση.
Γ) Όταν ένα σώμα συγκρουστεί
ελαστικά με δεύτερο σώμα πολύ μεγάλης μάζας (τοίχος), το μέτρο της ορμής του
παραμένει σταθερό.
Δ) Δύο σώματα που συγκρούονται
μετωπικά και ελαστικά ανταλλάσσουν ταχύτητες όταν έχουν ίσες μάζες.
6. Όταν δύο σώματα συγκρούονται ελαστικά, τότε :
Α) Η ορμή του κάθε σώματος
μεταβάλλεται.
Β) Η ορμή του συστήματος
διατηρείται.
Γ) Η κινητική ενέργεια του κάθε
σώματος μεταβάλλεται.
Δ) Η κινητική ενέργεια του
συστήματος διατηρείται.
7. Σώμα μάζας m κινείται οριζόντια με ταχύτητα
μέτρου υ. Στην πορεία του συγκρούεται ελαστικά με κατακόρυφο τοίχο. Η μεταβολή
στην ορμή του σώματος έχει μέτρο :
Α) 0
Β) mυ/2 Γ) mυ Δ) 2mυ
Ποια είναι η σωστή απάντηση;
8.Κατά την
κεντρική ελαστική κρούση δύο σφαιρών:
Β) Η κινητική ενέργεια της κάθε σφαίρας διατηρείται.
Γ) Η μεταβολή της ορμής της μιας σφαίρας είναι αντίθετη από τη μεταβολή της
ορμής της άλλης
Δ) Η μεταβολή της κινητικής ενέργειας της μιας σφαίρας είναι ίση με τη
μεταβολή της κινητικής ενέργειας της άλλης.
9. Κατά την ελαστική κρούση δύο σωμάτων
Α) Η ολική κινητική ενέργεια του
συστήματος παραμένει σταθερή.
Β) Η κινητική ενέργεια κάθε σώματος
παραμένει σταθερή.
Γ) Η κινητική ενέργεια του
συστήματος αυξάνεται.
Δ) Η κινητική ενέργεια του
συστήματος μειώνεται.
10.
Σώμα Α μάζας m κινείται πάνω σε οριζόντιο επίπεδο και συγκρούεται
με ταχύτητα υ με σώμα Β μάζας
2m που είναι ακίνητο. Η κρούση είναι πλαστική.
α. Η ταχύτητα του συσσωματώματος είναι υ΄ = υ/2.
β. Ο λόγος της τελικής κινητικής ενέργειας του συστήματος προς την αρχική
του σώματος Α είναι Κ΄/ Κ = 1/ 4.
γ. Ο λόγος της τελικής ορμής του σώματος Α προς την αρχική ορμή του είναι
pΑ΄/pΑ
= 1.
11. Κατά την πλαστική κρούση δύο σωμάτων η
μηχανική ενέργεια του συστήματος
α) παραμένει σταθερή.
β) αυξάνεται.
γ) μειώνεται.
12.
Δύο σώματα Α και Β κινούνται πάνω στην ίδια ευθεία προς αντίθετες κατευθύνσεις
με ταχύτητες ίσων μέτρων και συγκρούονται κεντρικά. Μετά τη σύγκρουση τα δύο
σώματα παραμένουν ενωμένα και ακίνητα. Ποιες από τις επόμενες προτάσεις είναι
σωστές και γιατί;
Α) Πριν την κρούση η ολική ορμή του συστήματος ήταν μηδέν.
Β) Τα δύο σώματα έχουν ίσες μάζες.
Γ) Η ολική κινητική ενέργεια του συστήματος έμεινε αμετάβλητη κατά την
κρούση.
ΑΣΚΗΣΕΙΣ
1)
Τη χρονική στιγμή t0 = 0, το Σ1 εκτοξεύεται προς τα αριστερά, με ταχύτητα μέτρου |υ1| = 4m/s, ενώ τη χρονική στιγμή t1 =0,8s, το Σ3 εκτοξεύεται προς τα δεξιά, με ταχύτητα μέτρου |υ3| =5m/s. Οι ταχύτητες είναι μετρημένες από έναν ακίνητο παρατηρητή, οι εκρήξεις διαρκούν αμελητέο χρονικό διάστημα και η αντίσταση του αέρα θεωρείται αμελητέα.
α) Ποια είναι η ταχύτητα του τμήματος Σ2-Σ3, αμέσως μετά την εκτόξευση του Σ1;
β) Ποια είναι η ταχύτητα του Σ2 αμέσως μετά την εκτόξευση του Σ3;
γ) Ποιο είναι το συνολικό ποσό της ενέργειας που εκλύθηκε από τα εκρηκτικά, αν το 45,3% αυτής έγινε θερμότητα και ακτινοβολία;
δ) Ποια θα είναι η μετατόπιση κάθε σώματος τη χρονική στιγμή t2 = 2,8s;
ε) Ποια θα έπρεπε να είναι η ταχύτητα εκτόξευσης του Σ3 ώστε το Σ2 να ακινητοποιηθεί;
2)
Δύο σφαιρικά σώματα Σ1 και Σ2 με μάζες m1 και m2 αντίστοιχα κινούνται πάνω σε οριζόντιο δάπεδο και συγκρούονται κεντρικά και πλαστικά.Ελάχιστα πριν την σύγκρουση τα δύο σώματα κινούνται με αντίθετη φορά,έχοντας ταχύτητες μέτρων υ1=20m/s και υ2 .Η μεταβολή της ορμής της σφαίρας Σ2 κατά την κρούση έχει αλγεβρική τιμή
Δp2=6Kgm/s.Ως
θετική φορά στη διεύθυνση της κίνησης των δύο σωμάτων, θεωρούμε αυτή της υ1. Η χρονική διάρκεια της κρούσης είναι Δt=0,1s.Η κρούση τελειώνει στη θέση
που αρχίζει.Το συσσωμάτωμα αμέσως μετά την κρούση έχει ταχύτητα ίδιας φοράς με αυτή της υ1 και
ακινητοποιείται αφού διανύσει διάστημα S=6,25m.
Δίνεταιg=10m/s2 .
Να υπολογίσετε:
α. Το
μέτρο της μέσης δύναμης που άσκησε το
σώμα Σ2 στο Σ1.
β. Το
μέτρο της ταχύτητας του συσσωματώματος
που προκύπτει από την κρούση.
γ. Τη
μάζα m1 του
σώματος Σ1
δ. Aν ο ποσοστό μεταβολής της κινητικής
ενέργειας του σώματος Σ2,κατά
την κρούση είναι
-75% να βρεθεί το μέτρο υ2 της ταχύτητας του Σ2 ελάχιστα
πριν την κρούση.
3)

Ένα σώμα μάζας m ηρεμεί πάνω σε οριζόντιο επίπεδο. Σε μια στιγμή t=0, δέχεται την επίδραση μιας μεταβλητής οριζόντιας δύναμης,η τιμή της οποίας μεταβάλλεται με το χρόνο, όπως στο παρακάτω σχήμα,

πότε αναπτύσσεται τριβή μεταξύ σώματος και δαπέδου, με μέγιστη τιμή Τορ=Τολ=10Ν.
α. Ποιος ο αρχικός ρυθμός μεταβολής της ορμής του σώματος (μόλις δεχτεί την δύναμη F);
β. Να υπολογιστεί η ορμή και ο ρυθμός μεταβολής της ορμής του σώματος τη χρονική στιγμή t1=4s.
γ. Πόση είναι η κινητική ενέργεια του σώματος τη χρονική στιγμή t2=8s;
δ. Να βρεθεί ο ρυθμός με τον οποίο η δύναμη F μεταφέρει ενέργεια στο σώμα, τη χρονική στιγμή t3=16s, καθώς και ο ρυθμός με τον οποίο η μηχανική ενέργεια μετατρέπεται σε θερμική εξαιτίας της τριβής, την ίδια στιγμή, αν το σώμα έχει μάζα m=2kg.
Δίνεται g=10m/s
4)

Α) Σε λείο οριζόντιο επίπεδο ηρεμεί ένα σώμα. Σε μια στιγμή t0=0 ασκείται στο σώμα αυτό μια σταθερή οριζόντια δύναμη F, μέτρου F=4Ν.
- Να υπολογιστεί η ορμή του σώματος τη χρονική στιγμή t1=5s.
- Να κάνετε τη γραφική παράσταση F-t και να υπολογίστε το εμβαδόν του χωρίου που σχηματίζεται μεταξύ γραφικής παράστασης και άξονα των χρόνων. Σε τι συμπέρασμα καταλήγετε;
Β) Επαναλαμβάνουμε το πείραμα, αλλά τώρα η ασκούμενη δύναμη F, είναι μεταβλητή, το μέτρο της οποίας μεταβάλλεται με το χρόνο, σύμφωνα με την εξίσωση F=4t (S.Ι.).
- Να υπολογιστεί η ορμή του σώματος τη χρονική στιγμή t1=5s.
- Να κάνετε τη γραφική παράσταση της ορμής του σώματος σε συνάρτηση με το χρόνο, μέχρι της στιγμή t2=6s και να βρείτε την κλίση της καμπύλης που θα πάρετε, τη στιγμή t1.
5)

Ένα σώμα Α μάζας m εκτοξεύεται σε οριζόντιο επίπεδο και μετά από λίγο συγκρούεται με ένα δεύτερο ακίνητο σώμα Β, με αποτέλεσμα η ορμή του σώματος Α να μεταβάλλεται σε συνάρτηση με το χρόνο, όπως στο διπλανό σχήμα.
- Ποια χρονική στιγμή συνέβη η κρούση μεταξύ των σωμάτων Α και Β; Να δικαιολογήσετε την απάντησή σας.
- Να υπολογιστεί η τριβή που αναπτύσσεται μεταξύ του σώματος Α και του οριζοντίου επιπέδου.
- Πόση ορμή αποκτά το σώμα Β, μετά την κρούση;
- Ποια χρονική στιγμή t1, το σώμα Α κινείται προς τα αριστερά με ορμή μέτρου 10kg∙m/s;
- Αν m=2kg, να υπολογιστούν:
α) Η μηχανική ενέργεια η οποία μετατρέπεται σε θερμική, εξαιτίας της τριβής, πριν την κρούση.
β) Ο ρυθμός με τον οποίο η κινητική ενέργεια του σώματος Α μετατρέπεται σε θερμική τη χρονική στιγμή t1.
6)

Σε λείο οριζόντιο επίπεδο ηρεμεί ένα σώμα Α. Σε μια στιγμή t0=0 στο σώμα Α ασκείται μια σταθερή οριζόντια δύναμη μέτρου F=1,5Ν, με φορά προς τα δεξιά, μέχρι τη στιγμή t1=6s, όπου η δύναμη καταργείται. Τη στιγμή t2=7s το σώμα Α συγκρούεται πλαστικά με δεύτερο σώμα Β μάζας m2=1kg, το οποίο κινείται αντίθετα από το Α με ταχύτητα μέτρου 1m/s.
- Να υπολογιστεί η ορμή του σώματος Α ελάχιστα πριν την κρούση.
- Ποια η ορμή του συσσωματώματος αμέσως μετά την κρούση.
- Αν η ταχύτητα του συσσωματώματος μετά την κρούση έχει μέτρο V=2m/s, να βρεθούν:
α) Η μάζα του Α σώματος.
β) Η μεταβολή της ορμής κάθε σώματος, η οποία οφείλεται στην κρούση.
γ) Η απώλεια της κινητικής ενέργειας κατά την πλαστική κρούση μεταξύ των δύο σωμάτων.


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου